Thursday, 14 May 2009
Atom interferometry in the blogosphere
Again I am busy. Sometime I intend to do a post about the truncated Wigner method of simulating quantum and thermal fluctuations. In the meantime here is an interesting blog post about atom interferometry and Steve Chu.
Monday, 4 May 2009
Bose-Einstein condensates, quasi-condensates and Tonks gasses
In my research I am largely concerned with 1D gasses of bosons (particles with integer spin). One of the reasons I model 1D is that it is quicker and easier than running 3D simulations/ doing 3D calculations. However, 1D systems display many effects that 3D systems do not. For the purposes of this article, I will assume that the atoms interact with each other via a repulsive force.


At a critical temperature (very close to absolute zero), ideal 3D bose gasses will condense into a Bose-Einstein condensate, where many atoms occupy the same quantum state. Fluctuations in the density of the gas are suppressed and there is phase coherence across the system (the condensate may be described by a complex-valued wavefunction). Such a system is exhibits the famous quantum-mechanical particle-wave duality, but on a (nearly) macroscopic scale.
This paper (arxiv) shows the phase diagram (below) of a 1D bose gas is somewhat more complicated.
In an infinite-sized 1D system, a Bose gas cannot condense into such a Bose-Einstein condensate, since phase fluctations destroy the coherence across the system. In this case, the density fluctations are still supressed, and the system is called a quasi-condensate. In a finite system, at sufficiently low temperature and high atom number, the phase fluctuations may be of such large wavelength that they are bigger than the size of the system itself, and the gas behaves exactly as a true Bose-Einstein condensate.
This is not the entire picture; if a gas is sufficiently dilute, or the repulsive interactions are strong, the atoms can be thought of as localised individual particles. In 1D, the particles cannot pass each other, as in higher dimensional systems. As a consequence of this, the atoms gain some properties of Fermi atoms (such Fermionised bosons cannot occupy the same position state - however, unlike Fermions, they can still occupy the same momentum state). This system is called a Tonks gas.
Moreover, when the inter-particle collisions in a Tonks gas are elastic, the system becomes integrable (it has "regular motion"), and the atoms cannot obtain a thermal equilibrium since the energy cannot divide itself equally between the particles. This system acts like a quantum Newton's cradle (this Newton's cradle gif animation is taken from Wikipedia).

The moral of this post is that there is a lot to consider when modelling a 1D Bose gas.
Labels:
Atomic Physics,
Bose-Einstein condensate,
Cold Atoms,
Physics
Monday, 27 April 2009
Cold atoms in the news
Too busy to do a proper post at the moment. In the mean-time, look at this article on the BBC website, (featuring an interview with a young atom optician).
Saturday, 18 April 2009
Cold atoms probe fundamental physics
High energy physics, e.g., at CERN, promises to discover physics beyond the standard model. However, it is not necessary to expend all this energy and money to probe fundamental physics. One can do so in tabletop experiments on cold atoms, molecules and ions.
This current interest has reminded me of work by Ed Hinds to measure the electron electric dipole moment by observing the change in the energy levels of cold molecules on the application of a magnetic field. A non-zero value of such a quantity would show physics beyond the standard model. The Imperial College website has several pages of lucid explanation for the layperson here. Here is a chart from their website showing how precise they are trying to get.
Thursday, 9 April 2009
The boring world of Niels Bohr

All this is to precede an addendum to my previous post about Bohr atoms: I neglected to consider interactions of Rydberg atoms with low frequency black-body radiation, which should cause stimulated transitions to nearby Rydberg states, thus decohering the quantum state; this could possibly be the principle cause of the classical type radiation.
Saturday, 4 April 2009
Entanglement and free will
A colleague recently directed me to this paper (arxiv here), about entanglement and its philosophical consequences, by John Conway, of whom I was previously aware as a pure mathematician, and Simon Kochen.
The paper considers a system of two entangled spin-1 particles in separate locations, such that the total spin of the particles is zero. The authors assume that the observer (A) of one particle has free will to chose a set of axes in which to measure the squared components of the spin of the particle (i.e., he can make a choice of which axes to chose independent of his past history), and an observer of the other particle (B) has free will to measure the spin of this particle in one direction.
Furthermore, they assume the observers to be in motion such that A makes his measurement before B in A's inertial frame, but after B in B's inertial frame (temporal order is not invariant in relativity). The authors conclude that if we assume that the choices of A and B are free, then, in the same sense, the particles make a free choice (they give measurements independent of their past histories).
For more details, in addition to the original paper, see the recent notice to the AMS and this explanatory article. Also, John Conway is giving some lectures on the subject, the videos of which are being put online here.
Saturday, 21 March 2009
Rydberg Bohr atoms
Inspired by this post on the Uncertain Principles blog, and a talk I attended by Barry Dunning, I have recently become interested in Rydberg Bohr atoms. When quantum theory was in its infancy, Bohr proposed that electrons orbit atomic nucleii in certain classical orbits, much as planets orbit the Sun in our solar system. However, the biggest problem for this theory was that classical physics requires that charged particles, such as electrons, radiate light as they accelerate, and consequently lose energy. Such electrons would therefore be expected to spiral into the atomic nucleus whilst continuously emitting radiation.
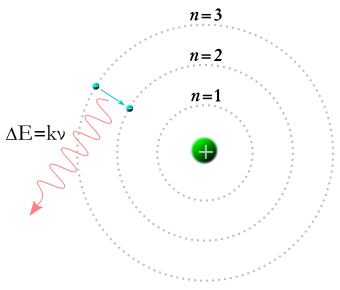
Modern quantum mechanics tells us that electrons are not localised in space, but behave rather as waves, and their classical properties such as positions, momenta, energies and angular momenta may be only fuzzily defined (i.e., we can only know probabilistically the outcomes of their measurements). The electrons only radiate light when they are stimulated to by interacting with passing light (stimulated emission), or by interacting with the vacuum (spontaneous emission).
We expect quantum physics to reduce to classical physics in some limit; the nature of this limit is not well established - it could be the limit of large objects or many interactions with the environment. Rydberg atoms are atoms with an electron excited to a high energy state, such that the electron is likely to be found far away from the nucleus of the atom. In these two recent papers, atoms are excited to a superposition of such Rydberg states so that their outer electrons are fairly localised in space, and orbit the atomic nucleii, much in the way of the Bohr atom. This is a classical limit, in the sense that the electron follows a classical trajectory, however, spontaneous emission of light from such atoms is fairly well suppressed (since the rate of emission scales in inverse proportion of the energy cubed). It actually seems that the lifetimes of the orbits are limited by the dephasing of the wavepacket (i.e., the orbit's quantum nature becomes important), rather than by spontaneous emission.
Nevertheless, it would be interesting to look at the spontaneous emission as a function of the expected angular momentum or position, and compare it to the classical radiation from an orbiting charge. Actually, I think I may attempt these calculations myself. I would normally be loath to describe my research ideas in a public forum incase I get scooped; however, I suspect that no-one reads this blog anyway.
I conclude with a picture of a Bohr atom taken from Wikipedia:

Friday, 13 March 2009
Cold Atoms in Optical Lattices
 When I told my mum that my research involved optical lattices she said, "lattices - like in pastry". In fact, optical lattices are means of trapping atoms in regular positions by overlapping laser beams. Trapping atoms in such an ordered way has many uses - for instance as a quantum register, or to simulate the behaviour of electrons in metals and semi-conductors (where the lattice is provided by an array of positively charged ions).
When I told my mum that my research involved optical lattices she said, "lattices - like in pastry". In fact, optical lattices are means of trapping atoms in regular positions by overlapping laser beams. Trapping atoms in such an ordered way has many uses - for instance as a quantum register, or to simulate the behaviour of electrons in metals and semi-conductors (where the lattice is provided by an array of positively charged ions). Immanuel Bloch has already written a very good popular-science article about quantum gasses in optical lattices, so I will not re-write it here, but I will take the opportunity to discuss some of the theoretical approaches to modelling such systems. I been asked questions about the Bose-Hubbard model by interested experimentalists, so I will start there:
When there are relatively few atoms in each lattice site, and the lattice is sufficiently strong compared with the energy of the atoms, then the Hubbard (for Fermions) or Bose-Hubbard (for Bosons) model describes the system effectively. I will concentrate on the Bosonic case, since that is closest to my interests. In this model, the atoms’ behaviour is governed by a tunneling parameter between neighbouring lattice sites, and a parameter describing the interaction between atoms in the same site (see Dieter Jaksch et al. Phys. Rev. Lett. 81 3108 for details).
In the Bose-Hubbard system there is a quantum phase transition between superfluid behaviour (the atoms flow freely between lattice sites) and Mott insulator behaviour (atoms become trapped in individual sites) when the tunneling between lattice sites becomes sufficiently weak. The insulating phase is useful when we want, for instance, one atom to be localised in each lattice site to use as a quantum register.
When the number of atoms becomes large, the Hilbert space of the Bose-Hubbard model may become too large to be practical. In this case, in the superfluid (weak lattice) phase, the Gross-Pitaevskii equation describing the mean-field of all the atoms as a single wavefunction is a good model (see Morsch and Oberthaler's review article). I will take this opportunity to publicise my boss's paper on what happens when, for large atom numbers, you start with a superfluid and then ramp up the lattice potential. It turns out that Mott insulator states are hard to achieve in this case. It may be possible to achieve a Mott insulator with large atom numbers, but it looks like doing so will be a challenge.
Much more physics has been done, of course, in optical lattices than I have described. However, I hope this post has given a flavour of the subject.
Sunday, 8 March 2009
Hello world
Hello, my name is Andrew, I am a theoretical atomic physicist, and I have spied a "gap in the market" for a blog with the theme of physics of ultra-cold atoms. Inspired by blogs about what are popularly perceived to be the sexier areas of physics (e.g., Cosmic Variance), I think that the exciting and rapidly expanding area of ultra-cold physics is worthy of a blog, and perhaps I am the man to start it. Note that like all bloggers I reserve the right to be self indulgent and blog about other subjects that interest me, even if they are off topic.
A quick word on why the subject of ultra-cold atoms is one of the most interesting in physics:
Ultra-cold atoms are those cooled and trapped (usually by lasers) at a temperature close to absolute zero. At this temperature, the atoms obey the rules of quantum mechanics and may display the famous effects at which we all like to marvel, such as behaving as waves rather than particles, existing in two places at once, etc. Atoms may entangle with each other allowing amazing technologies that sound like science fiction, such as atomic teleportation, quantum computation and quantum cryptography. The Nobel prize in physics has been awarded to ultra-cold atomic physicists in 1997, 2001 and 2005. Notice that Steve Chu a Nobel prize winner in 1997 is Obama's new energy secretary.
I hope that the world is as interested in this stuff as much as me. If you work in the field of atomic physics, or are just interested in the subject, if you would like to write posts for this blog let me know using the comments section.
Subscribe to:
Posts (Atom)



